El objetivo de este blog es convertirlo en un portafolio virtual en el cual se pueden observar algunas actividades diseñadas utilizando las Tecnologías de la Comunicación y la Información ‘‘Tics’’.
domingo, 4 de noviembre de 2012
sábado, 3 de noviembre de 2012
Derivadas
Definicion:
La derivada d euna funcion es la medida dela rapidez con la que cambia el valor de dicha funcion segun cambie el valor de su variable independiente.
Es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología, o en ciencias sociales como la Economía y la Sociología.
La derivada d euna funcion es la medida dela rapidez con la que cambia el valor de dicha funcion segun cambie el valor de su variable independiente.
Es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología, o en ciencias sociales como la Economía y la Sociología.
sábado, 9 de junio de 2012
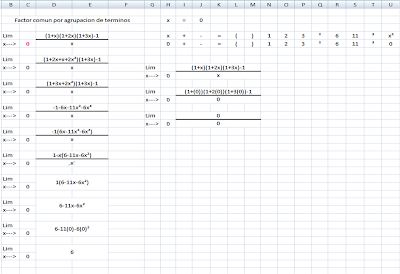
Limites
Limites es : Cuando una funcion f esta definida para un valor x proximo aun numero dado puede ser 5 y si cuando el valor de x se acerca al numero 5 ,se encuentra que los valores de f(x) se acercan mas y mas a un numero real en este caso L se dice entonces que L es limite de y=f(x) cuando x tiende a el numero dado en este caso 5 .
Lim F(x) =L
x-->5
Lim F(x) =L
x-->5
sábado, 31 de marzo de 2012
5.4 Teoremas del Seno y Coseno
Teorema de los senos
Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.
Teorema del coseno
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
5.3 Relaciones Trigonométricas
El seno: la razón entre el cateto opuesto y la hipotenusa:
5.2 teorema de pitagoras
El teorema de pitagoras expresa una relación entre los cuadrados de las medidas de los lados de un triangulo rectángulo.
Situación del problema:
Una ventana mide 8,94 cm verticalmente y 4,00 cm de largo, teniendo en cuenta el teorema de pitágoras y estos datos, resuelve el siguiente problema:
- ¿que longitud tiene la horizontal de esta ventana ?
5.1 Historia de la trigonometria
La historia de la trigonometría se remonta a las primeras matemáticas conocidas, en Egipto y Babilonia. Los egipcios establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, hasta los tiempos de la Grecia clásica no empezó a haber trigonometría en las matemáticas. En el siglo II a. C. el astrónomo Hiparco de Nicea realizó una tabla trigonométrica para resolver triángulos. Comenzando con un ángulo de 71° y yendo hasta 180 °C con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. Esta tabla es similar a la moderna tabla del seno. No se sabe con certeza el valor de r utilizado por Hiparco, pero sí se sabe que 300 años más tarde el astrónomo Tolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico sexagesimal (base 60) de los babilonios.
martes, 27 de marzo de 2012
4.6 Triángulo Rectángulo
El triangulo rectángulo es aquel en el que uno de sus ángulos es recto y los otros dos son agudos.Los lados de este triangulo se llaman catetos y el otro es la hipotenusa
4.2 Teoremas de Pitágoras
El teorema de pitagoras expresa una relación entre los cuadrados de las medidas de los lados de un triangulo rectángulo.
a2 , b2, c2 son las areas de cuadrados de los lados a,b,c respectivamente.
4.1 Definición de triángulo
Un triangulo es un polígono de tres lados.
Un triangulo se determina por tres segmentos de recta que se denominan lados y por tres puntos no alineados que se llaman vértices.
Los vértices se representan con una letra mayúscula y los lados con letra minúscula la misma letra de los vértices opuestos.
Un triangulo se determina por tres segmentos de recta que se denominan lados y por tres puntos no alineados que se llaman vértices.
Los vértices se representan con una letra mayúscula y los lados con letra minúscula la misma letra de los vértices opuestos.
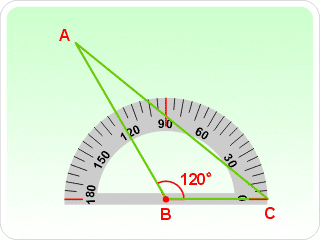
2.2 Ángulos y clases de Ángulos.
Un angulo Es la figura formada por 2 semirrectas que parten de un mismo punto. Las semirectas se llaman lados y el punto común vértice.
Clases de ángulos:
Angulo está formado por el cruce de dos rectas perpendiculares que forman la cuarta parte de una revolución, es decir, 90º.
Angulo obtuso:un angulo obtuso tiene una abertura mayor , a la del angulo recto, correctamente 180°
Angulo agudo: una angulo agudo tiene una abertura menor ala de un angulo recto.
Angulo plano: es aquel cuyos lados son semirrectas opuestas, ademas el angulo es la mitad de una revolución, es decir 180°.
existen otros tipos de ángulos como los adyacentes, consecutivos,opuestos por el vértice ,complementarios y suplementarios.Los ángulos consecutivos tienen el vértice y un lado en común.
Los ángulos adyacentes son consecutivos y suplementarios (suman 180º).Los ángulos opuestos por el vértice tienen como lados semirrectas opuesta.Los ángulos complementarios suman 90º.Los ángulos suplementarios suman 180º.
2.3 Mediatriz y Bisectriz
Mediatriz y Bisectriz
La mediatriz de un segmento es la recta perpendicular a dicho segmento que pasa por el punto medio.
La bisectriz de un ángulo es la recta que pasa por el centro del ángulo.
2.4 Recta Paralela y Recta Perpendicular
rectas paralelas y rectas perpendiculares
Dos rectas son paralelas si tienen el mismo vector director o la misma pendiente.
Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.
Dos rectas son perpendiculares si sus vectores directores son perpendiculares.
3.3 Nombres de Algunos Polígonos
| Algunos poligonos | |||
| Nombre | Lados | Forma | Ángulo interior |
|---|---|---|---|
| Triángulo (o trígono) | 3 | 60° | |
| Cuadrilátero (o tetrágono) | 4 | 90° | |
| Pentágono | 5 | 108° | |
| Hexágono | 6 | 120° | |
| Heptágono (o Septágono) | 7 | 128.571° | |
| Octágono | 8 | 135° | |
| Nonágono (or eneágono) | 9 | 140° | |
| Decágono | 10 | 144° | |
| Endecágono (or undecágono) | 11 | 147.273° | |
| Dodecágono | 12 | 150° | |
| Tridecágono | 13 | 152.308° | |
| Tetradecágono | 14 | 154.286° | |
| Pentadecágono | 15 | 156° | |
| Hexadecágono | 16 | 157.5° | |
| Heptadecágono | 17 | 158.824° | |
| Octadecágono | 18 | 160° | |
| Eneadecágono | 19 | 161.053° | |
| Icoságono | 20 | 162° | |
| Triacontágono | 30 | 168° | |
| Tetracontágono | 40 | 171° | |
| Pentacontágono | 50 | 172.8° | |
| Hexacontágono | 60 | 174° | |
| Heptacontágono | 70 | 174.857° | |
| Octacontágono | 80 | 175.5° | |
| Eneacontágono | 90 | 176° | |
| Hectágono | 100 | 176.4° | |
| Chiliágono | 1,000 | 179.64° | |
| Miriágono | 10,000 | 179.964° | |
| Megágono | 1,000,000 | ~180° | |
| Googológono | 10100 | ~180° | |
| n-ágono | n | (n-2) × 180° / n | |
Suscribirse a:
Comentarios (Atom)